随机过程

发表于 | 分类于 | 阅读次数

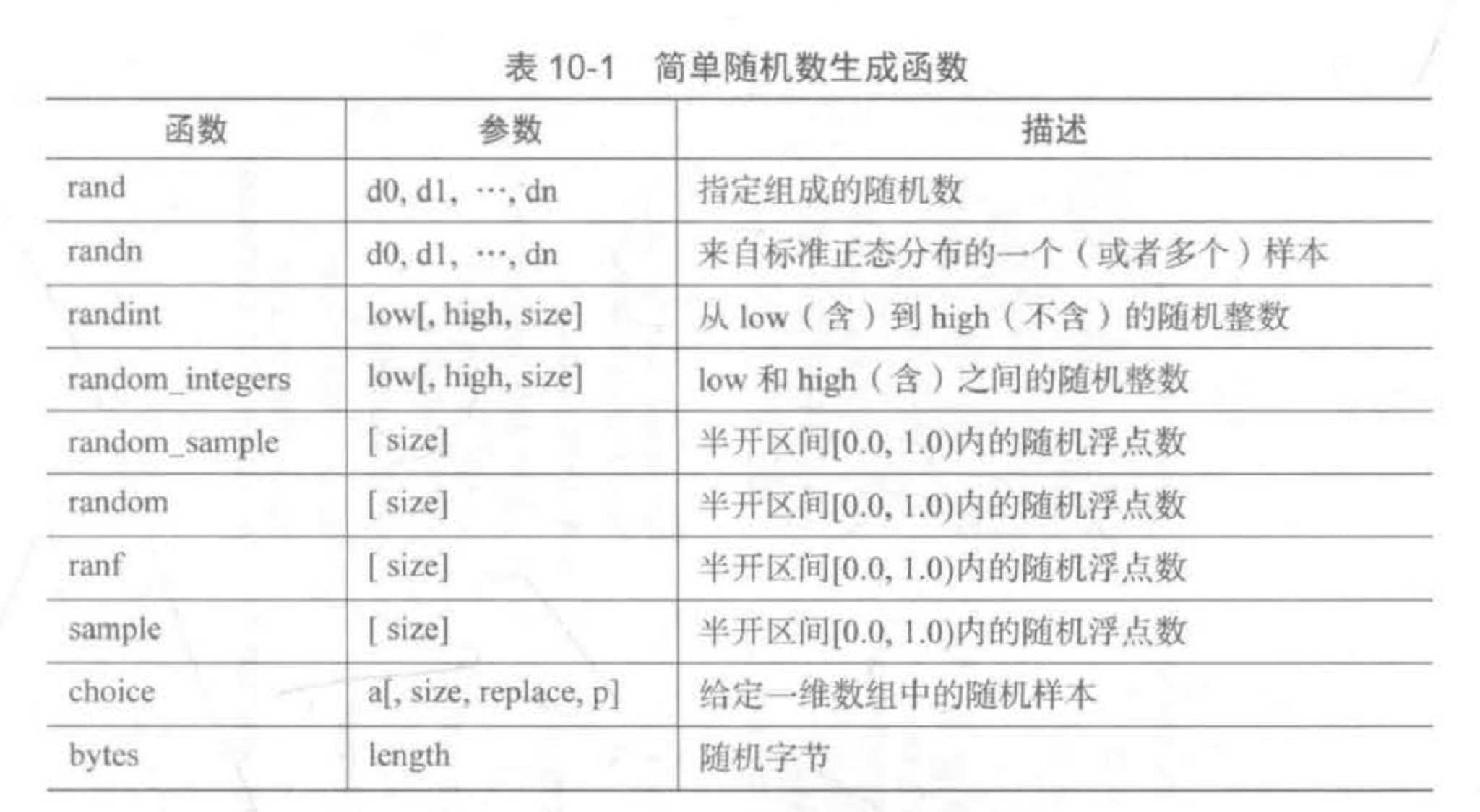
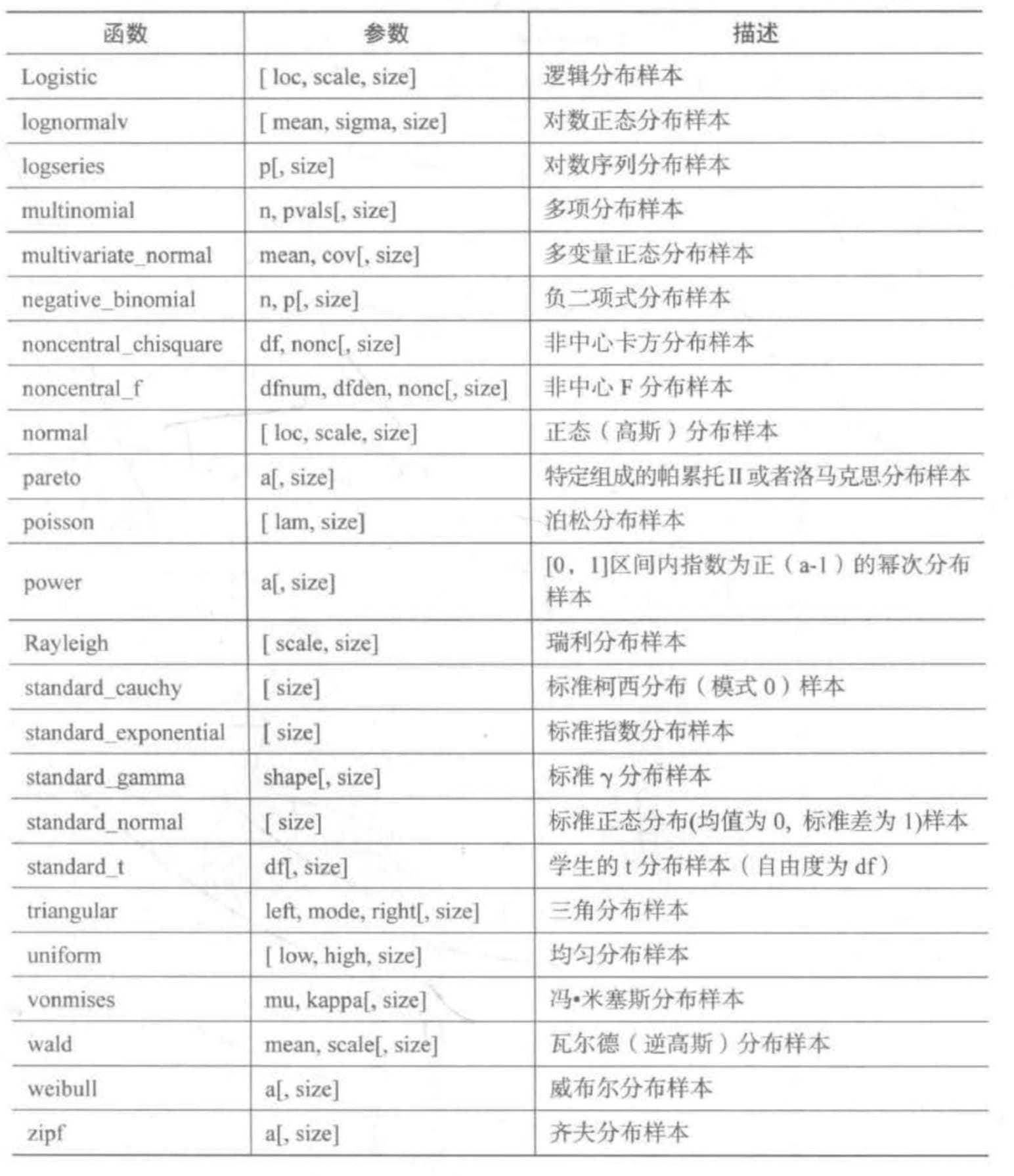
期权定价所用的Black-Scholes-Meron设置

$S_T=S_0exp((r-\frac12\sigma^2)T+\sigma\sqrt Tz)$

ST ：T日的指数水平 r ：恒定无风险短期利率 σ ：S的恒定波动率（= 收益率的标准差） z：标准正态分布随机变量 模拟的几何布朗运动

1
2
3
4
5
6
S0 = 100  # initial value
r = 0.05  # constant short rate
sigma = 0.25  # constant volatility
T = 2.0  # in years
I = 10000  # number of random draws
ST1 = S0 * np.exp((r - 0.5 * sigma ** 2) * T + sigma * np.sqrt(T) * np.random.standard_normal(I))

##随机过程 随机过程是一个随机变量序列,随机数的选取一般不是独立的,依赖于前几次选取的结果.

明天的过程值只依赖于今天的过程状态， 而不依赖其他任何 “历史” 状态． 甚至不依赖整个路径历史。无记忆过程

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
x0 = 0.05
kappa = 3.0
theta = 0.02
sigma = 0.1

T = 2.0
I = 10000
M = 50
dt = T / M


def srd_euler():
    xh = np.zeros((M + 1, I))
    x1 = np.zeros_like(xh)
    xh[0] = x0
    x1[0] = x0
    for t in range(1, M + 1):
        xh[t] = (xh[t - 1]
                 + kappa * (theta - np.maximum(xh[t - 1], 0)) * dt
                 + sigma * np.sqrt(np.maximum(xh[t - 1], 0)) * np.sqrt(dt)
                 * np.random.standard_normal(I))
    x1 = np.maximum(xh, 0)
    return x1

平方根扩散的精确离散化 

1
2
3
4
5
6
7
8
9
def srd_exact():
    x2 = np.zeros((M + 1, I))
    x2[0] = x0
    for t in range(1, M + 1):
        df = 4 * theta * kappa / sigma ** 2
        c = (sigma ** 2 * (1 - np.exp(-kappa * dt))) / (4 * kappa)
        nc = np.exp(-kappa * dt) / c * x2[t - 1]
        x2[t] = c * random.noncentral_chisquare(df, nc, size=I)
    return x2

##随机波动率 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
S0 = 100.
r = 0.05
v0 = 0.1
kappa = 3.0
theta = 0.25
sigma = 0.1
rho = 0.6
T = 1.0
# 为了说明两个随机过程之间的相关性，我们需要确定相关矩阵的柯列斯基分解：
corr_mat = np.zeros((2, 2))
corr_mat[0, :] = [1.0, rho]
corr_mat[1, :] = [rho, 1.0]
cho_mat = np.linalg.cholesky(corr_mat)
cho_mat
# array([[ 1. ,  0. ],
#        [ 0.6,  0.8]])
# 在开始模拟随机过程之前， 我们为两个过程生成整组随机数， 指数过程使用第0组，波动性过程使用第1组：
M = 50
I = 10000
ran_num = random.standard_normal((2, M + 1, I))
# 对于以平方根扩散过程类型建模的波动性过程， 我们使用欧拉格式， 考虑相关性参数：
dt = T / M
v = np.zeros_like(ran_num[0])
vh = np.zeros_like(v)
v[0] = v0
vh[0] = v0
for t in range(1, M + 1):
    ran = np.dot(cho_mat, ran_num[:, t, :])
    vh[t] = (vh[t - 1] + kappa * (theta - np.maximum(vh[t - 1], 0)) * dt
             + sigma * np.sqrt(np.maximum(vh[t - 1], 0)) * np.sqrt(dt)
             * ran[1])
    v = np.maximum(vh, 0)

# 对于指数水平过程, 我们也考虑相关性，使用几何布朗运动的精确欧拉格式：
S = np.zeros_like(ran_num[0])
S[0] = S0
for t in range(1, M + 1):
    ran = np.dot(cho_mat, ran_num[:, t, :])
    S[t] = S[t - 1] * np.exp((r - 0.5 * v[t]) * dt +
                             np.sqrt(v[t]) * ran[0] * np.sqrt(dt))

# 这说明了平方根扩散中使用欧拉格式的另一项优势：相关性很容易一致性地处理， 因为我们只提取标准正态随机数。 没有一种棍合方法（对指数使用欧拉格式， 对波动性过程使用基于非中心卡方分布的精确方法）能够实现相同的效果。

跳跃扩散

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
S0 = 100.
r = 0.05
sigma = 0.2
lamb = 0.75
mu = -0.6
delta = 0.25
T = 1.0
# 为了模拟跳跃扩散,需要生成3组（独立）随机数：
M=50
I=10000
rj=lamb*(np.exp(mu+0.5*delta**2)-1)
S=np.zeros((M+1,I))
S[0]=S0
sn1=random.standard_normal((M+1,I))
sn2=random.standard_normal((M+1,I))
poi=random.poisson(lamb*dt,(M+1,I))
for t in range(1,M+1,1):
    S[t]=S[t-1]*(np.exp((r-rj-0.5*sigma**2)*dt
                        +sigma*np.sqrt(dt)*sn1[t])
                        +(np.exp(mu+delta*sn2[t])-1)
                        *poi[t])
    S[t]=np.maximum(S[t],0)

##方差缩减 (sn - sn.mean()) / sn.std()