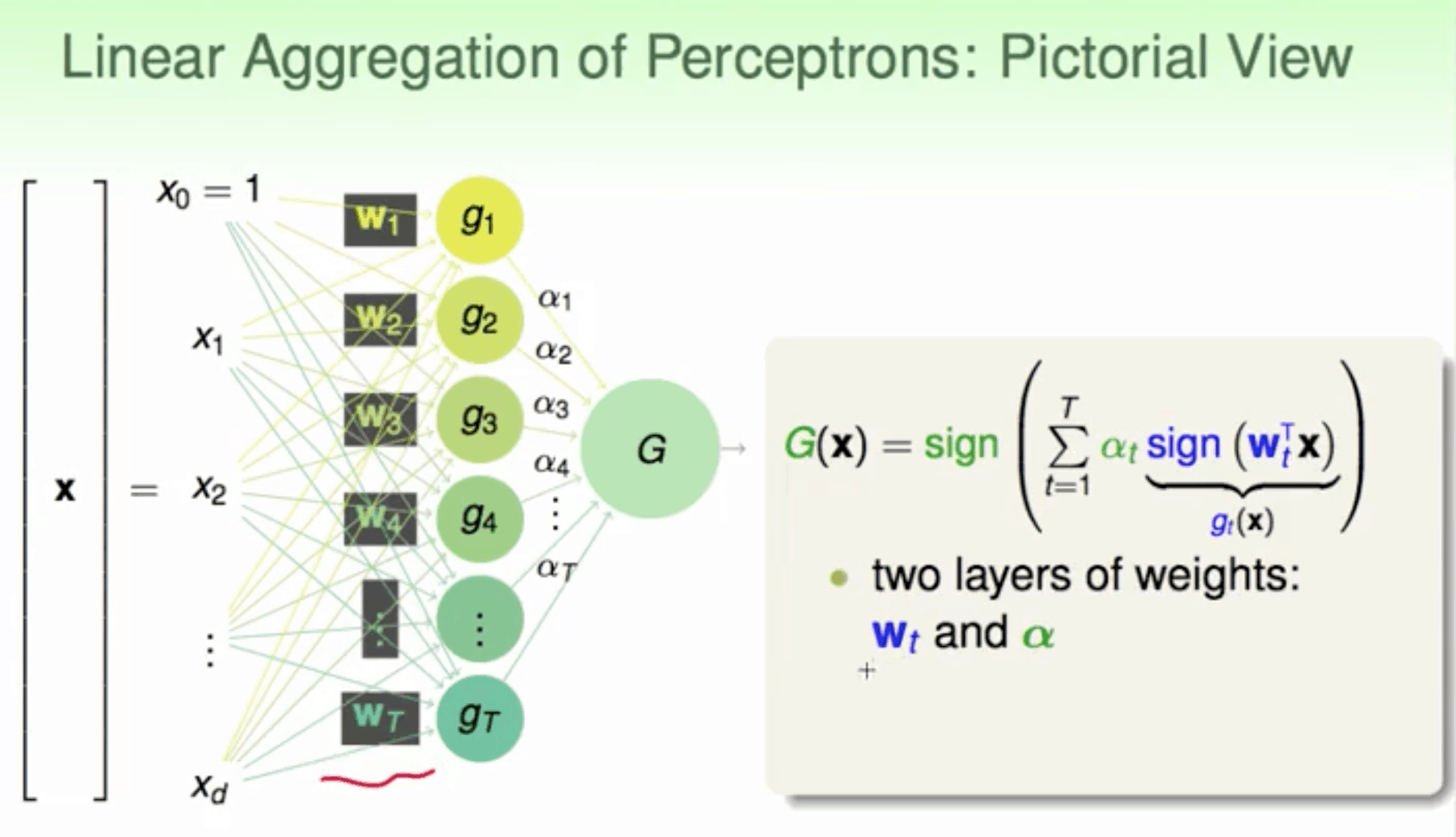
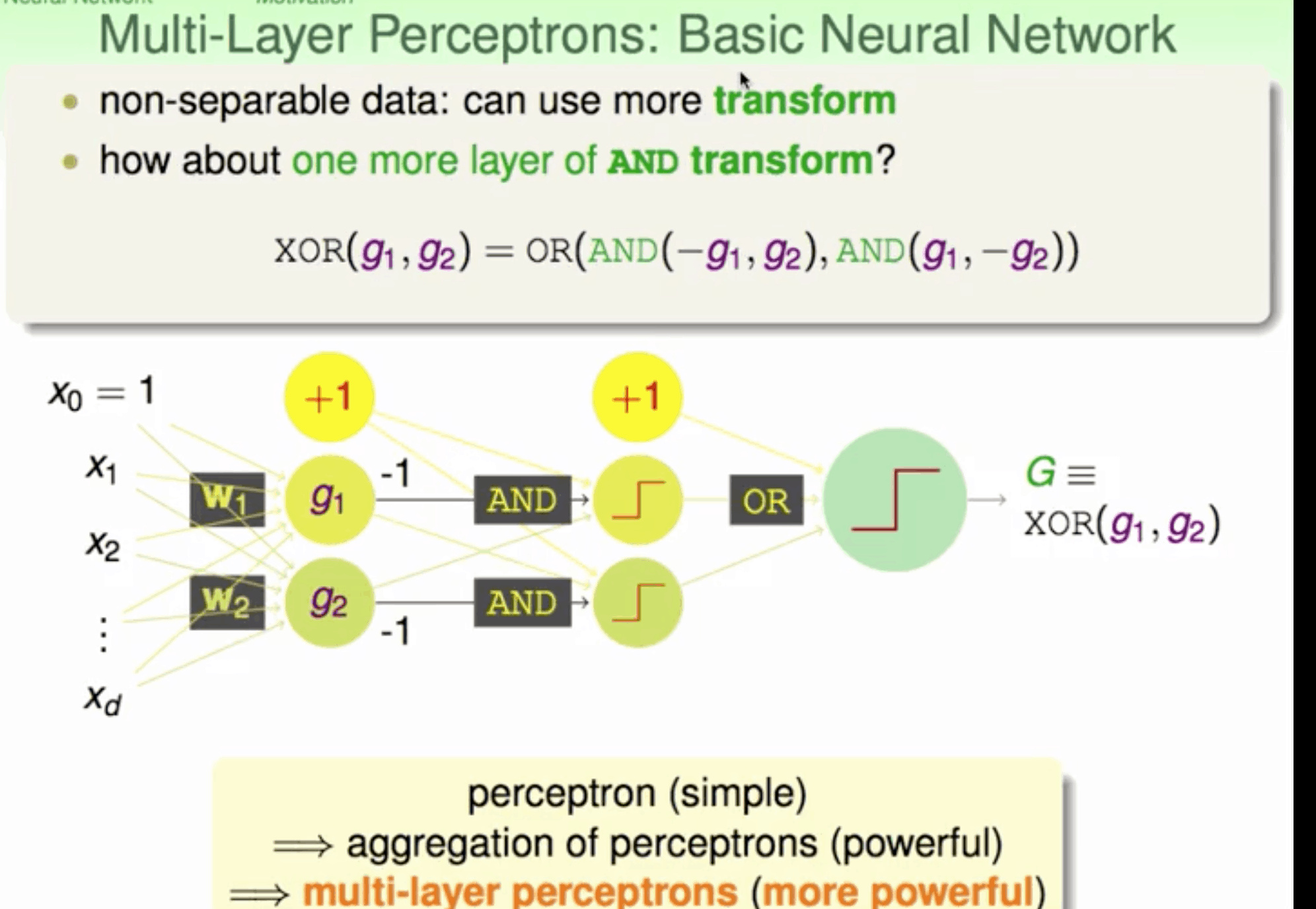
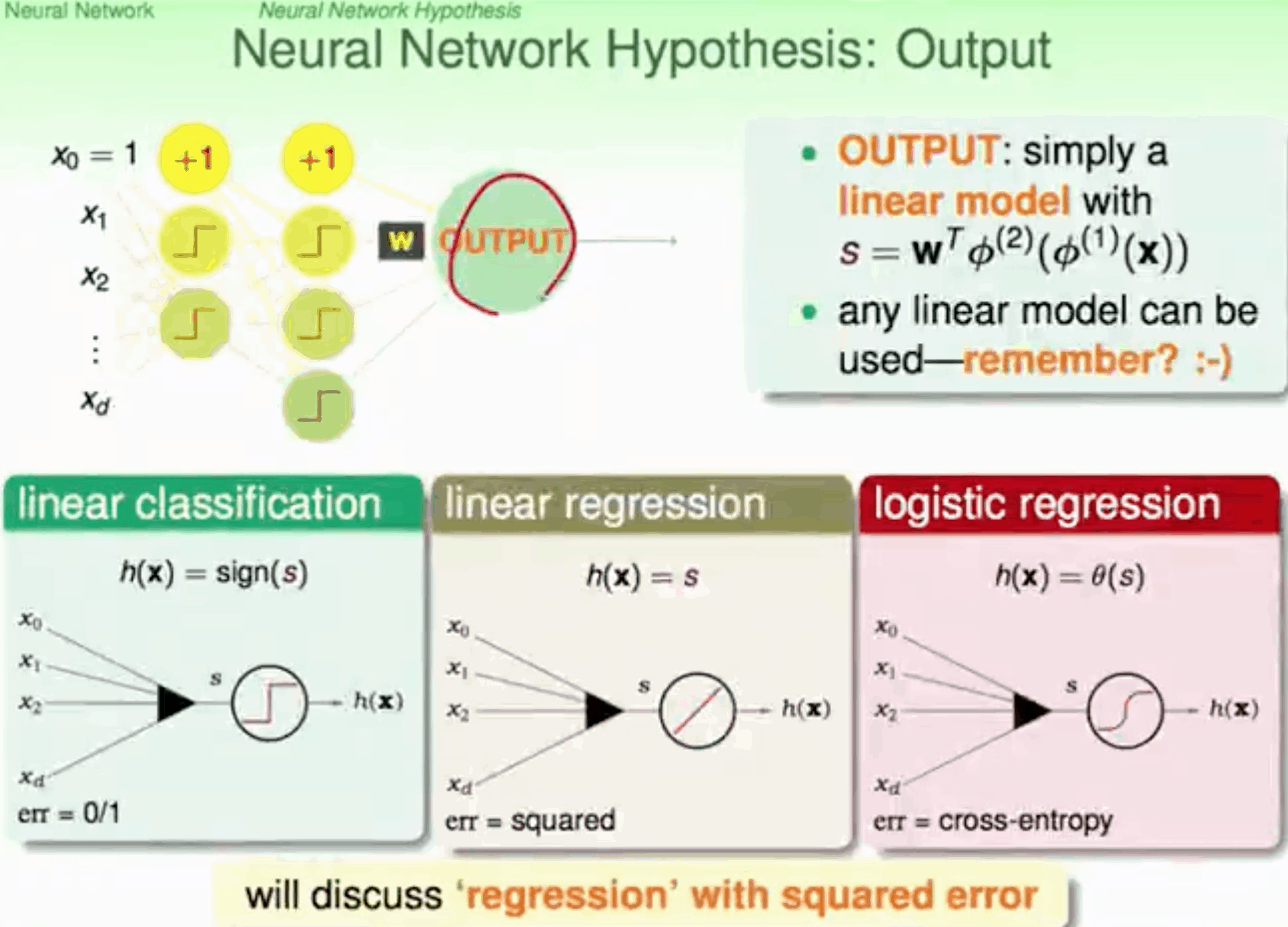
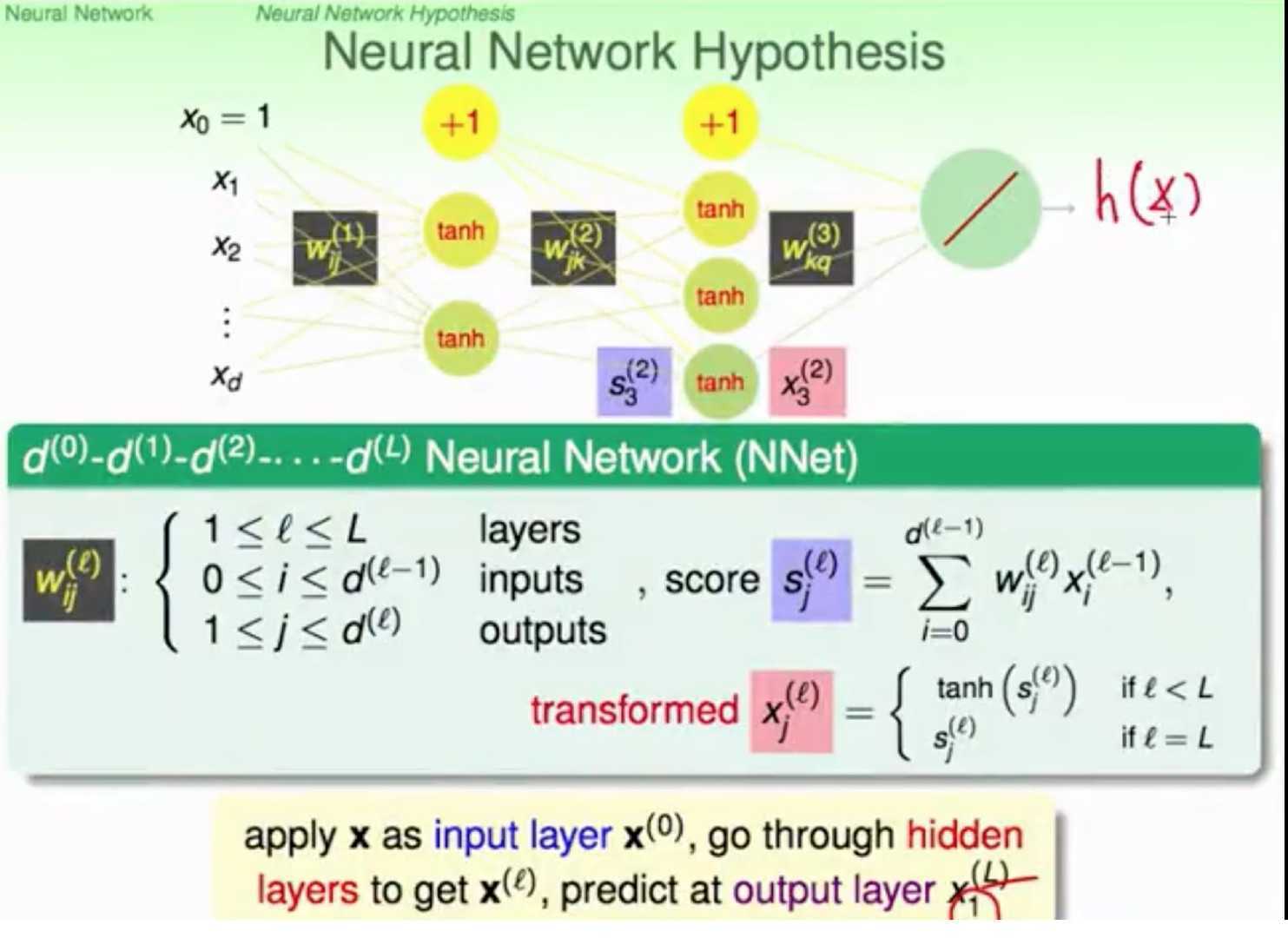
求W

损失函数

分类交叉熵
回归MSE

反向传播 backward propagation

\[cost=\frac12\left(\mathrm{真实值}-\mathrm{预测值}\right)^2\]

方便求导求 cost的min

梯度下降SGD 不断修正W $W\;=\;W\;-\;\frac{\partial\;cost}{\partial W}$

Example : 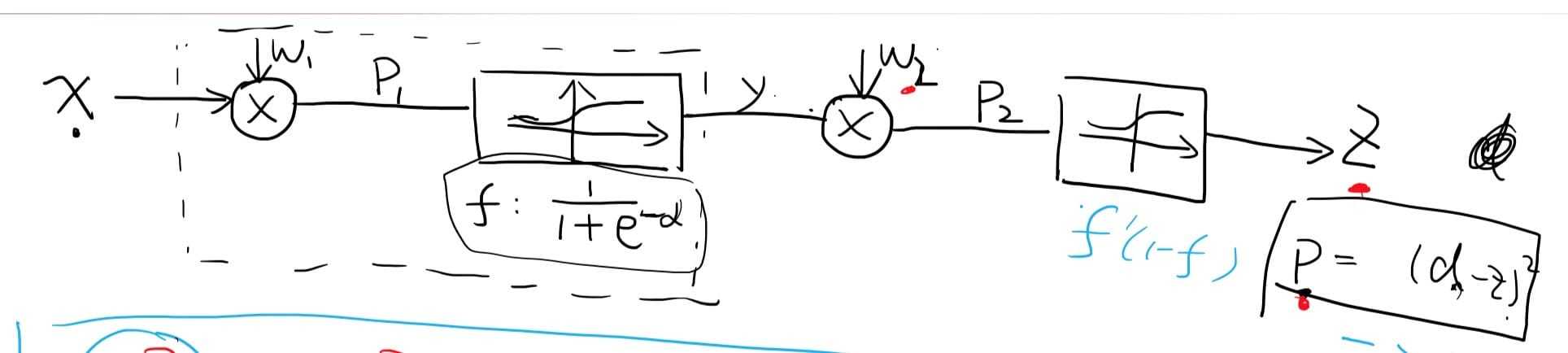目标求$\frac{\partial\;P}{\partial W_2},\frac{\partial\;P}{\partial W_1}$

链式偏导 $\frac{\partial\;P}{\partial W_2} = \frac{\partial\;P}{\partial Z}*\frac{\partial\;Z}{\partial W_2}$ 恒等变换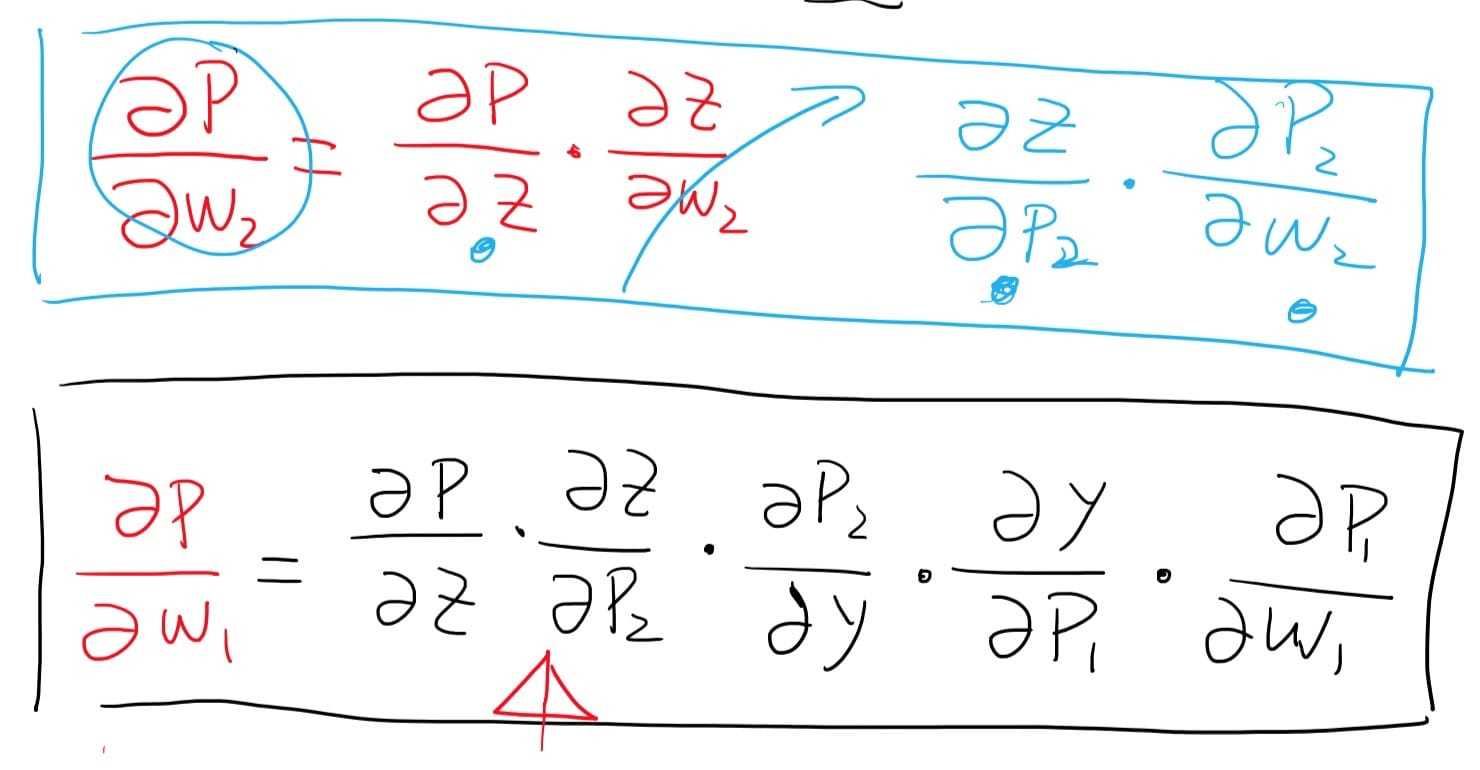整理一下

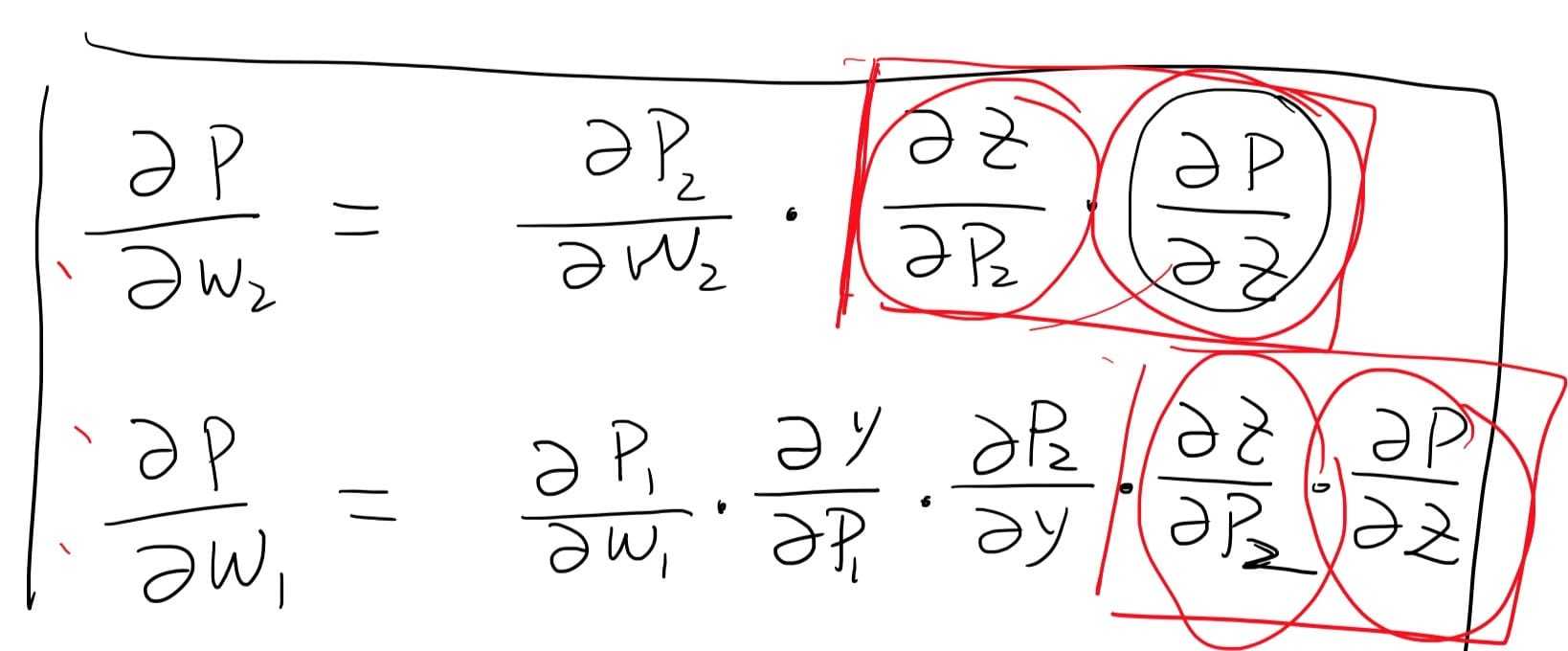
从后往前推导微分当网络复杂时偏导路径很多反向传播: 重复偏导的地方重复使用不再算省时间（链式偏导+动态规划）

优化NN

NN 结果对W初始值敏感一般选随机

复杂度神经网络中神经元的个数,权值的数量D O(VD)

dNN

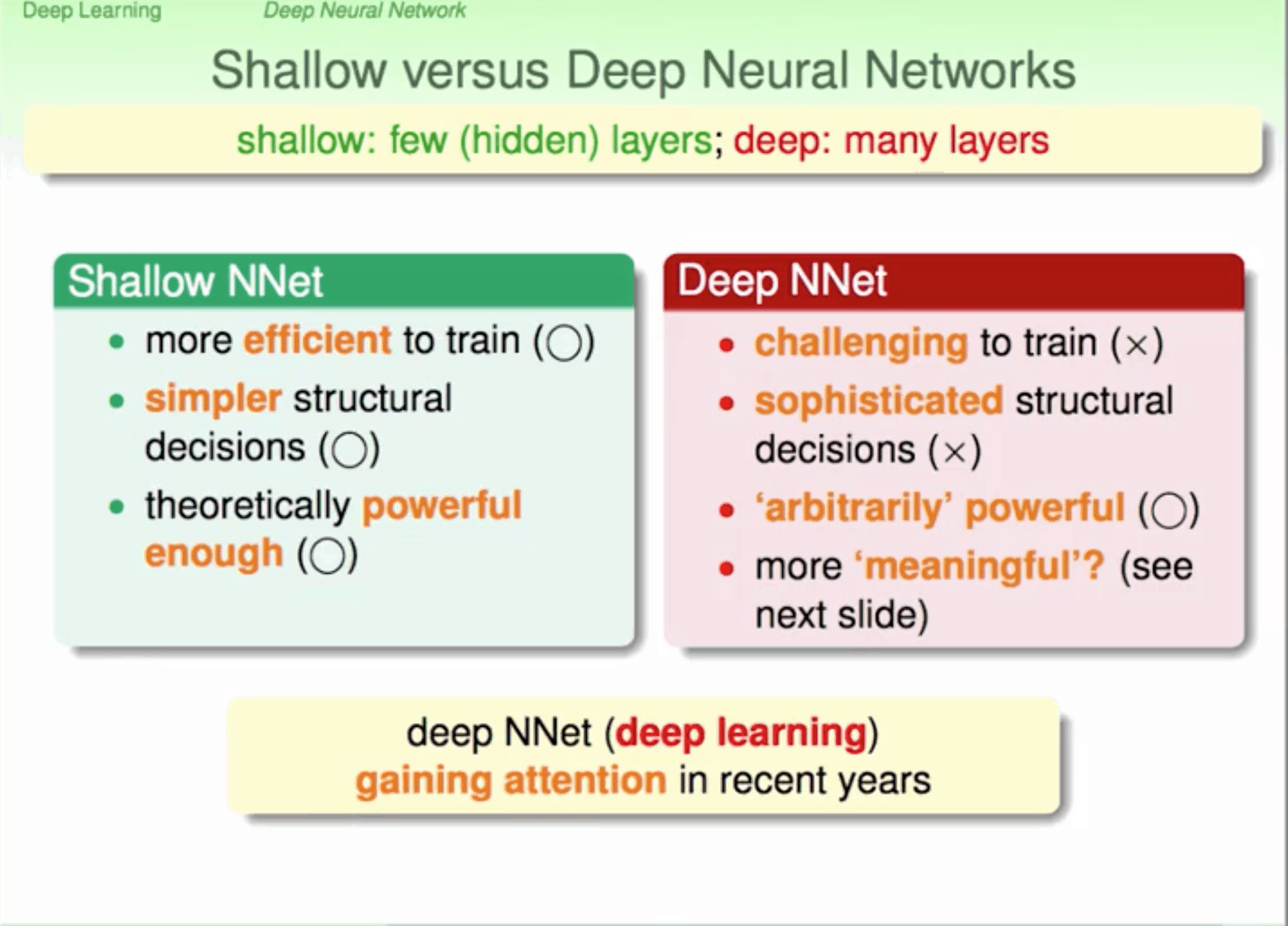
梯度消失

激活函数sigmoid将负无穷到正无穷的数映射到0和1之间神经网络的反向传播是逐层对函数偏导相乘，因此当神经网络层数非常深的时候，最后一层产生的偏差就因为乘了很多的小于1的数而越来越小，最终就会变为0，从而导致层数比较浅的权重没有更新，这就是梯度消失。此深层网络的学习就等价于只有后几层的浅层网络的学习

梯度爆炸

初始化权值过大，前面层会比后面层变化的更快，就会导致权值越来越大，梯度爆炸的现象就发生了

网络太深 -> 因为梯度反向传播中的连乘效应用ReLU取代sigmoid

Example

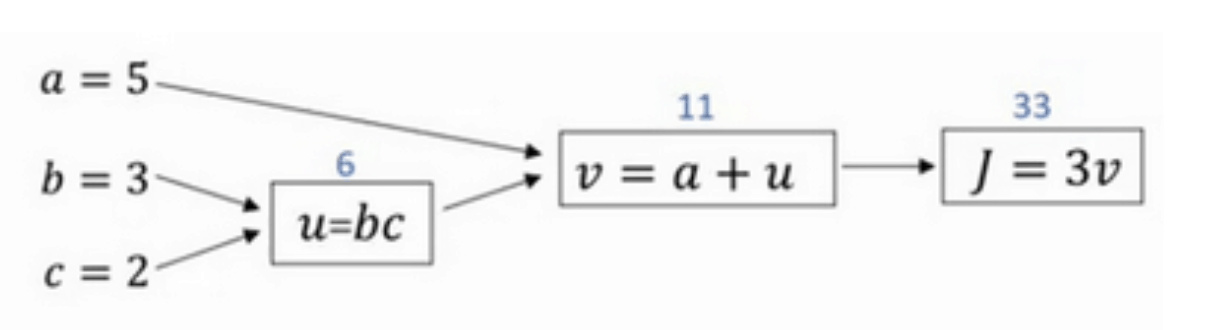
正向传播（Forward Propagation）

J(a,b,c)=3(a+bc)

反向传播 (Back Propagation)

即计算输出对输入的偏导数

首先计算J对参数a的偏导数。从计算图上来看，从右到左，J是v的函数，v是a的函数。则利用求导技巧，可以得到：

\[\frac{\partial J}{\partial a}=\frac{\partial J}{\partial v}\cdot \frac{\partial v}{\partial a}=3\cdot 1=3\]

根据这种思想，然后计算J对参数b的偏导数。从计算图上来看，从右到左，J是v的函数，v是u的函数，u是b的函数。可以推导：

\[\frac{\partial J}{\partial b}=\frac{\partial J}{\partial v}\cdot \frac{\partial v}{\partial u}\cdot \frac{\partial u}{\partial b}=3\cdot 1\cdot c=3\cdot 1\cdot 2=6\]

最后计算J对参数c的偏导数。仍从计算图上来看，从右到左，J是v的函数，v是u的函数，u是c的函数。可以推导：

\[\frac{\partial J}{\partial c}=\frac{\partial J}{\partial v}\cdot \frac{\partial v}{\partial u}\cdot \frac{\partial u}{\partial c}=3\cdot 1\cdot b=3\cdot 1\cdot 3=9\]