algorithm

发表于 | 分类于 | 阅读次数

动态规划

首先，动态规划问题的一般形式就是求最值。动态规划其实是运筹学的一种最优化方法，只不过在计算机问题上应用比较多，比如说让你求最长递增子序列呀，最小编辑距离呀等等。

既然是要求最值，核心问题是什么呢？求解动态规划的核心问题是穷举。因为要求最值，肯定要把所有可行的答案穷举出来，然后在其中找最值呗。

首先，动态规划的穷举有点特别，因为这类问题存在「重叠子问题」，如果暴力穷举的话效率会极其低下，所以需要「备忘录」或者「DP table」来优化穷举过程，避免不必要的计算。

而且，动态规划问题一定会具备「最优子结构」，才能通过子问题的最值得到原问题的最值。子问题间必须互相独立。

另外，虽然动态规划的核心思想就是穷举求最值，但是问题可以千变万化，穷举所有可行解其实并不是一件容易的事，只有列出正确的「状态转移方程」才能正确地穷举。

以上提到的重叠子问题、最优子结构、状态转移方程就是动态规划三要素。具体什么意思等会会举例详解，但是在实际的算法问题中，写出状态转移方程是最困难的，这也就是为什么很多朋友觉得动态规划问题困难的原因，我来提供我研究出来的一个思维框架，辅助你思考状态转移方程。

1
2
3
4
5
6
7
# 初始化 base case
dp[0][0][...] = base
# 进行状态转移
for 状态1 in 状态1的所有取值：
    for 状态2 in 状态2的所有取值：
        for ...
            dp[状态1][状态2][...] = 求最值(选择1，选择2...)
  • 自顶向下

是从上向下延伸，都是从一个规模较大的原问题比如说 f(20)，向下逐渐分解规模，直到 f(1) 和 f(2) 这两个 base case，然后逐层返回答案，这就叫「自顶向下」。

  • 自底向上

问题规模最小的 f(1) 和 f(2) 开始往上推，直到推到我们想要的答案 f(20)，这就是动态规划的思路

如何列出正确的状态转移方程

  • 确定 base case，这个很简单，显然目标金额 amount 为 0 时算法返回 0

  • 确定原问题和子问题中会变化的变量。由于硬币数量无限，硬币的面额也是题目给定的，只有目标金额会不断地向 base case 靠近，所以唯一的「状态」就是目标金额 amount。

  • 确定导致变量产生变化的行为。目标金额为什么变化呢，因为你在选择硬币，你每选择一枚硬币，就相当于减少了目标金额。所以说所有硬币的面值。

  • 明确 dp 函数/数组的定义。我们这里讲的是自顶向下的解法，所以会有一个递归的 dp 函数，一般来说函数的参数就是状态转移中会变化的量；函数的返回值就是题目要求我们计算的量。

    dp(n) 的定义：输入一个目标金额 n，返回凑出目标金额 n 的最少硬币数量。

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    26
    27
    28
    29
    30
    31
    32
    33
    34
    35
    36
    37
    38
    39
    40
    41
    42
    43
    44
    45
    46
    47
    48
    49
    50
    51
    52
    53
    54
    55
    56
    57
        def rob3(self, root: TreeNode) -> int:
        """
        二叉树数据
        :param nums:
        :return:
        """
        tree_res = {}
        if not root:
            return 0
  
        if not root.right and not root.left:
            return root.val
  
        def _rob(node: TreeNode) -> int:
            if not node:
                return 0
            if node in tree_res:
                return tree_res[node]
            #  选子
            choice_son = _rob(node.right) + _rob(node.left)
            # parent
            choice_parent = node.val + (0 if node.right is None else _rob(node.right.left) + _rob(node.right.right)) + (
                0 if node.left is None else _rob(node.left.left) + _rob(node.left.right))
  
            res = max(choice_parent, choice_son)
            tree_res[node] = res
            return res
  
        return _rob(root)
        
        
     def rob2(self, nums: List[int]) -> int:
        """
        环形数据
        :param nums:
        :return:
        """
  
        if not nums:
            return 0
        size = len(nums)
        if size == 1:
            return nums[0]
  
        def _get_dp(nums: List[int]) -> int:
            size = len(nums)
            if size == 1:
                return nums[0]
            dp = [0] * size
            dp[0] = nums[0]
            dp[1] = max(nums[0], nums[1])
            for i in range(2, size):
                dp[i] = max(dp[i - 2] + nums[i], dp[i - 1])
  
            return dp[size - 1]
  
        return max(_get_dp(nums[: - 1]), _get_dp(nums[1:]))

回溯算法

  • 路径：也就是已经做出的选择。

  • 选择列表：也就是你当前可以做的选择。

  • 结束条件：也就是到达决策树底层，无法再做选择的条件。

1
2
3
4
5
6
7
8
9
10
result = []
def backtrack(路径, 选择列表):
    if 满足结束条件:
        result.add(路径)
        return

    for 选择 in 选择列表:
        做选择
        backtrack(路径, 选择列表)
        撤销选择

其核心就是 for 循环里面的递归，在递归调用之前「做选择」，在递归调用之后「撤销选择」，特别简单。

def permute(self, nums: List[int]) -> List[List[int]]:
    results = []
    n = len(nums)

    def backtrack(select_list, track=None):
        if track is None:
            track = []
        if len(track) == n:
            results.append(track[:])
            return

        for s in select_list:
            if s in track:
                continue
            track.append(s)
            backtrack(select_list, track)
            track.pop()

    backtrack(nums)
    return results

写 backtrack 函数时，需要维护走过的「路径」和当前可以做的「选择列表」，当触发「结束条件」时，将「路径」记入结果集。

其实 DFS 算法就是回溯算法，BFS 相对 DFS 的最主要的区别是：BFS 找到的路径一定是最短的，但代价就是空间复杂度比 DFS 大很多

BFS

问题的本质就是让你在一幅「图」中找到从起点 start 到终点 target 的最近距离

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
def minDepth(self, root: TreeNode) -> int:
    if not root:
        return 0

    queue = collections.deque([(root, 1)])
    while queue:
        node, depth = queue.popleft()
        if not node.left and node.right:
            return depth
        if node.left:
            queue.append((node.left,depth+1))
        if node.right:
            queue.append((node.right,depth+1))

    return 0

二分

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
int binarySearch(int[] nums, int target) {
    int left = 0; 
    int right = nums.length - 1; // 注意

    while(left <= right) {
        int mid = left + (right - left) / 2; // 防止right+ left 溢出int
        if(nums[mid] == target)
            return mid; 
        else if (nums[mid] < target)
            left = mid + 1; // 注意
        else if (nums[mid] > target)
            right = mid - 1; // 注意
    }
    return -1;
}

为什么 while 循环的条件中是 <=，而不是 <？

答：因为初始化 right 的赋值是 nums.length - 1，即最后一个元素的索引，而不是 nums.length。

左侧极限

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
int left_bound(int[] nums, int target) {
    int left = 0, right = nums.length - 1;
    while (left <= right) {
        int mid = left + (right - left) / 2;
        if (nums[mid] < target) {
            left = mid + 1;
        } else if (nums[mid] > target) {
            right = mid - 1;
        } else if (nums[mid] == target) {
            // 别返回，锁定左侧边界
            right = mid - 1;
        }
    }
    // 最后要检查 left 越界的情况
    if (left >= nums.length || nums[left] != target)
        return -1;
    return left;
}

右侧极限

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
int right_bound(int[] nums, int target) {
    int left = 0, right = nums.length - 1;
    while (left <= right) {
        int mid = left + (right - left) / 2;
        if (nums[mid] < target) {
            left = mid + 1;
        } else if (nums[mid] > target) {
            right = mid - 1;
        } else if (nums[mid] == target) {
            // 别返回，锁定右侧边界
            left = mid + 1;
        }
    }
    // 最后要检查 right 越界的情况
    if (right < 0 || nums[right] != target)
        return -1;
    return right;
}

活动窗口

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
void slidingWindow(string s, string t) {
    unordered_map<char, int> need, window;
    for (char c : t) need[c]++;

    int left = 0, right = 0;
    int valid = 0; 
    while (right < s.size()) {
        // c 是将移入窗口的字符
        char c = s[right];
        // 右移窗口
        right++;
        // 进行窗口内数据的一系列更新
        ...

        /*** debug 输出的位置 ***/
        printf("window: [%d, %d)\n", left, right);
        /********************/

        // 判断左侧窗口是否要收缩
        while (window needs shrink) {
            // d 是将移出窗口的字符
            char d = s[left];
            // 左移窗口
            left++;
            // 进行窗口内数据的一系列更新
            ...
        }
    }
}

  • 当移动 right 扩大窗口，即加入字符时，应该更新哪些数据？

  • 什么条件下，窗口应该暂停扩大，开始移动 left 缩小窗口？

  • 当移动 left 缩小窗口，即移出字符时，应该更新哪些数据？

  • 我们要的结果应该在扩大窗口时还是缩小窗口时进行更新？

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
def lengthOfLongestSubstring(self, seq: str) -> int:
  if not seq:
    return 0
  left = 0
  res = 0
  win = defaultdict(int)
  for right in range(0, len(seq)):
    s = seq[right]
    win[s] += 1

    while win[s] > 1:
      d = seq[left]
      left += 1
      win[d] -= 1
      res = max(res, right - left + 1)

      return res

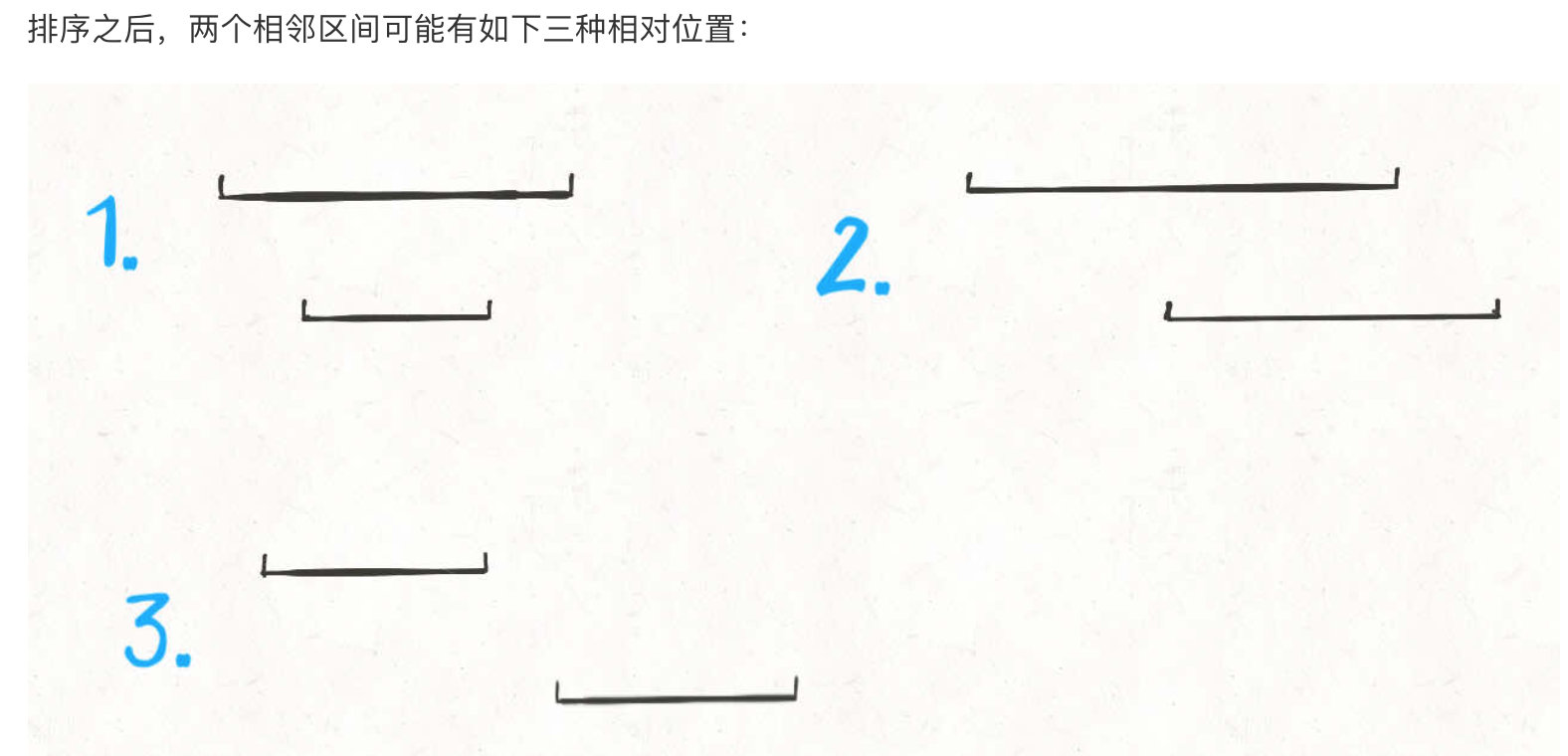
区间覆盖问题

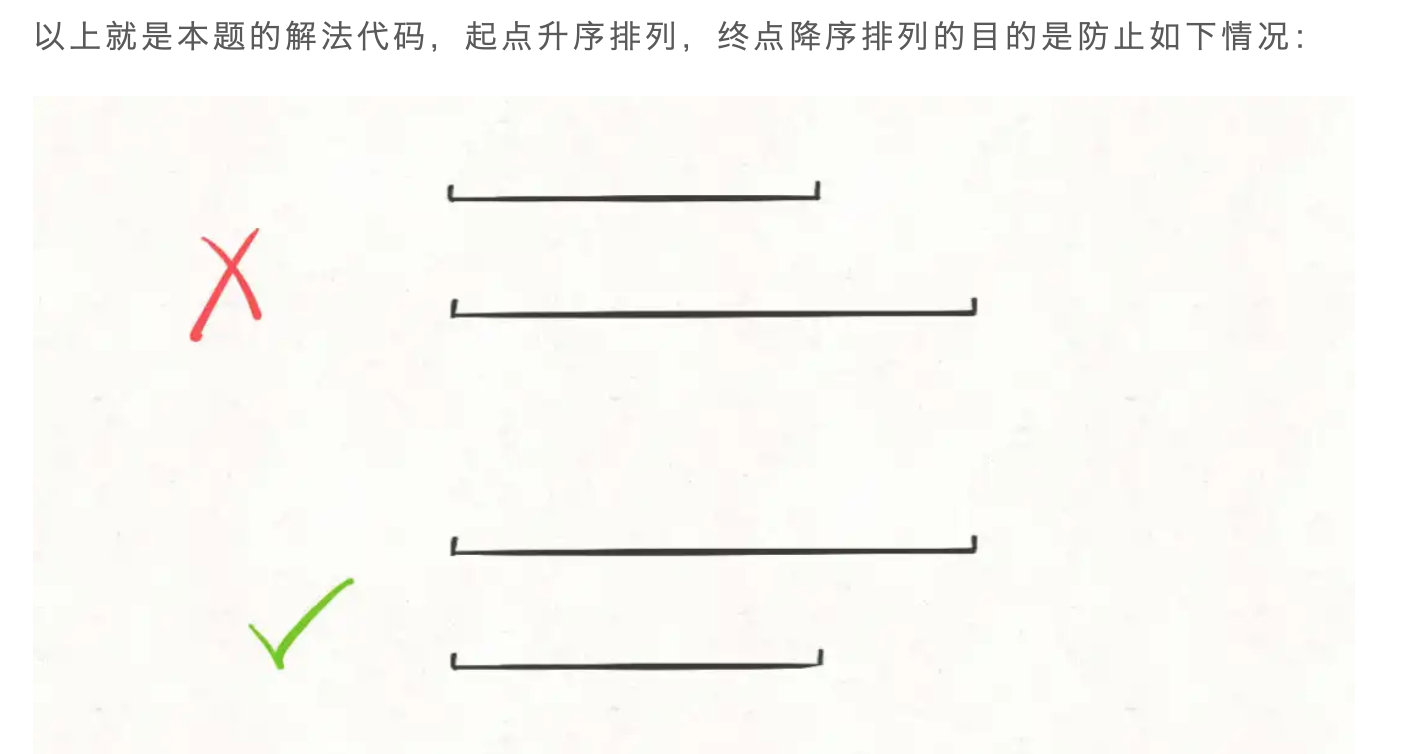
  • 排序。常见的排序方法就是按照区间起点排序，或者先按照起点升序排序，若起点相同，则按照终点降序排序。当然，如果你非要按照终点排序，无非对称操作，本质都是一样的。

  • 画图。就是说不要偷懒，勤动手，两个区间的相对位置到底有几种可能，不同的相对位置我们的代码应该怎么去处理。

image-20201227132759028

image-20201227132902760

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
    def removeCoveredIntervals(self, intervals: List[List[int]]) -> int:
        # Sort by start point.
        # If two intervals share the same start point
        # put the longer one to be the first.
        intervals.sort(key=lambda x: (x[0], -x[1]))
        count = 0

        prev_end = 0
        for _, end in intervals:
            # if current interval is not covered
            # by the previous one
            if end > prev_end:
                count += 1
                prev_end = end

        return count

    def merge(self, intervals: List[List[int]]) -> List[List[int]]:
        if len(intervals) == 0:
            return []

        intervals.sort(key=lambda x: (x[0], -x[1]))
        results = []
        for left, right in intervals:
            if not results or results[-1][1] < left:
                results.append([left, right])
            else:
                results[-1][1] = max(results[-1][1], right)
        return results