收益 从t-k 到 t 共k周期 简单收益率 \(\style{font-size:28px}{R_t\;=\;\frac{P_t}{P_{t\;-\;k}}-1\;=\;\frac{P_t\;-\;P_{t\;-k}}{P_{t\;-\;k}}}\) —
弱平稳性
弱平稳 序列{rt} 均值与cov(r1,r2)（相同周期内） var 不随时间改变 非平稳通过d次差分（$r_t-r_{t-1}$）近似平稳
自相关ACF
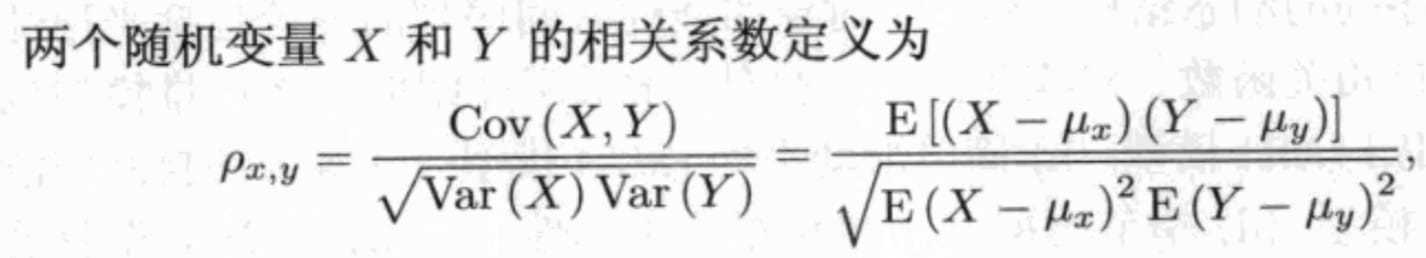
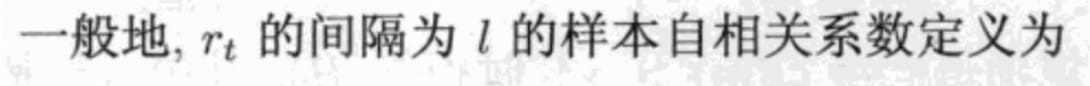
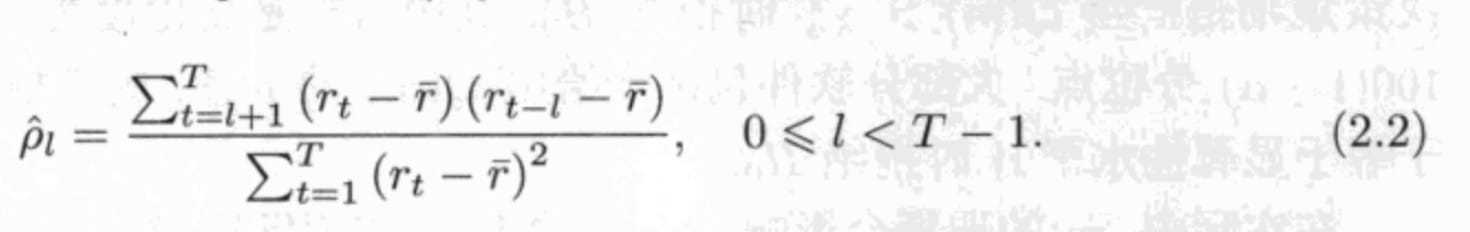
检验自相关
混成检验(Portmanteau Test)
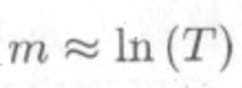
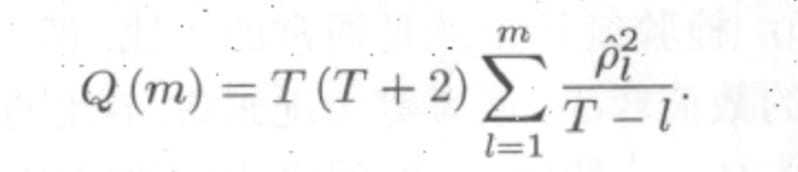
白噪声
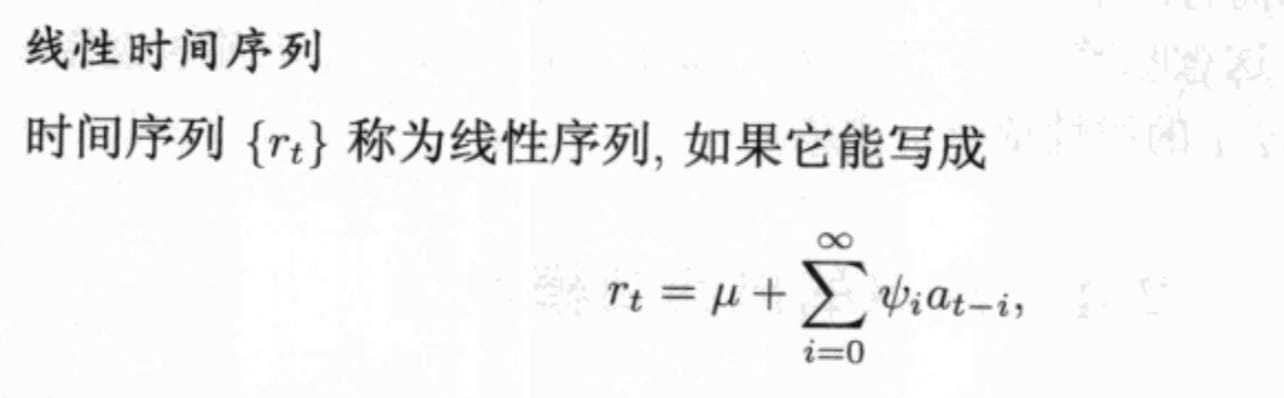
自回归模型AR(1)
AR(p) $r_t\;=\;\Phi_0+\Phi_1r_{t-1}+\dots+\Phi_pr_{t-p}+a_t$
AR性质
$E(r_t)\;=\;\frac{\Phi_0}{1-\Phi_1-\dots-\Phi_p}$
${\rho_l\;}=\;\Phi_1\rho_{l-1}+\Phi_2\rho_{l-2}+\dots+\Phi_p\rho_{l-p}$
$\because$ B是向后推移算子 $B\rho_l\;=\;\rho_{l-1}$ $\therefore 1-\Phi_1B-\Phi_2B^2-\dots\Phi_pB^p\;=\;0$ $\therefore 1-\Phi_1x-\Phi_2x^2-\dots\Phi_px^p\;=\;0$
$ if \left|x\right|>1 序列{\;r_t\;}平稳 解的倒数为特征根$ 所以所有特征根的模 < 1
定阶
p是未知
偏相关函数（PACF）p步截尾 信息准则 （AIC）适合的p使得aic最小 贝叶斯信息准则 BIC
##拟合优度 $R^2\;=\;1-\frac{var(\mathrm{残差})}{var(r_t)}$ — $0\leqslant R^2\;\leqslant1$ $R^2越大模型拟合越好$
预测
h是预测原点 l是预测步长 $r_{h+l}\;=\;\Phi_0+\Phi_1r_{h+l-1}+\dots+\Phi_pr_{h+l-p}+a_{h+l}$ —
移动平均MA
MA总是弱平稳
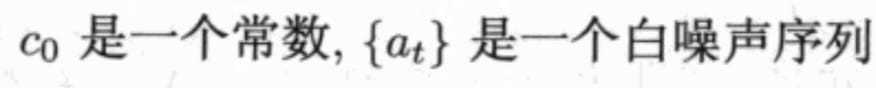
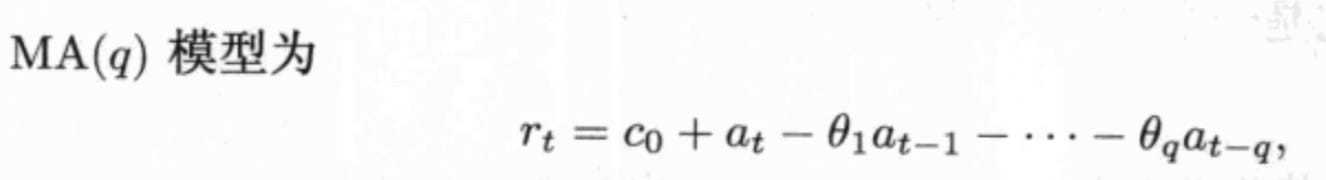定阶
acf q步截尾(q阶后自相关系数=0)
ARMA
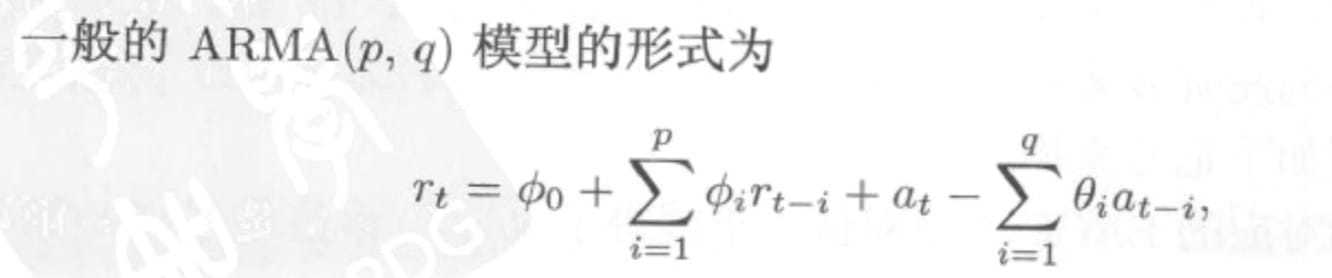p=0 => MA
所以所有特征根的模 < 1 才平稳
EACF AIC
ARIMA
价格序列通常是非平稳的 对数收益率是平稳的
单位根非平稳序列
ARIMA => AR特征根=1单位根非平稳序列 差分
若序列$y_t$ d重单位根非平稳序列 要d次差分（前-后) => d阶差分序列 $y_t$是ARIMA(p,d,q)过程
ADF 检验单位根 原假设是有单位根 非平稳