pca

发表于 | 分类于 | 阅读次数

很多机器学习的问题都会涉及到有着几千甚至数百万维的特征的训练实例。这不仅让训练过程变得非常缓慢，同时还很难找到一个很好的解， 我们接下来就会遇到这种情况。这种问题通常被称为维数灾难（curse of dimentionality）。

高维数据集处于非常稀疏的风险，大多数训练实例可能彼此远离。当然，这也意味着一个新实例可能远离任何训练实例，这使得预测的可靠性远低于较低维度，因为它们将基于更大的外推。 train-set 维数越多 overfit风险越大 降低维数，肯定加快训练速度，但并不总是会导致更好或更简单的解决方案;这一切都取决于数据集。

投影

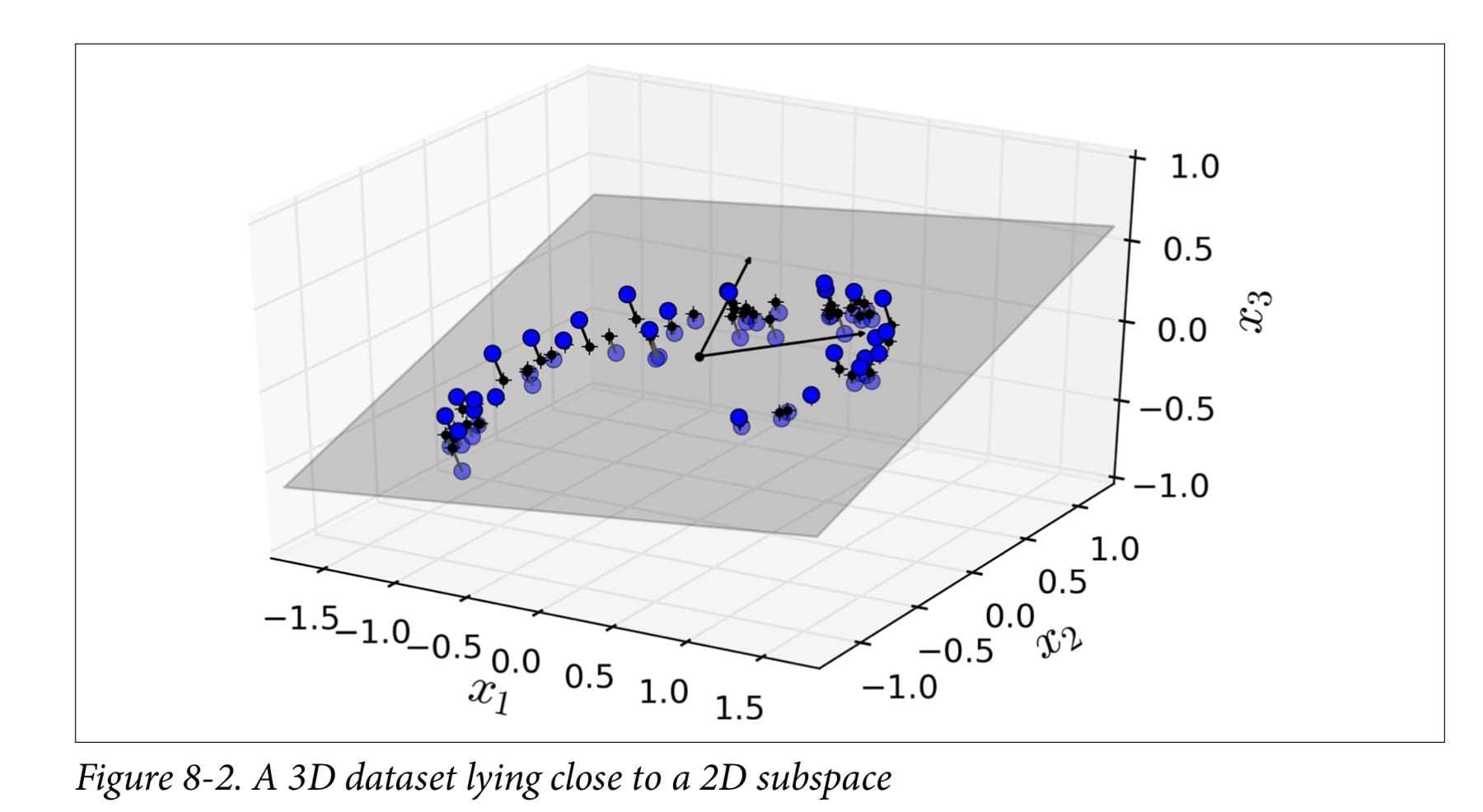
PCA

Principal Component Analysis (PCA) 首先识别与数据最接近的超平面，然后将数据投影到它上面

主成分分析 数据从原来的坐标系转换到了新的坐标系，新坐标系的选择是由数据本身决定的。 第一个新坐标轴选 择的是原始数据中方差最大的方向，第二个新坐标轴的选择和第一个坐标轴正交且具有最大方差的方向。 该过程一直重复，重复次数为原始数据中特征的数目。 我们会发现，大部分方差都包含 在最前面的几个新坐标轴中。我们可以忽略余下的坐标轴，即对数据进行了降维处理。

How to:

如何选择投影坐标轴方向（或者说 基）才能尽量保留最多的原始信息呢？一种直观的看法是：希望投影后的投影值尽可能分散。=> 方差

正交基 协方差=0

如何得到这些包含最大差异性的主成分方向 计算数据矩阵的 协方差矩阵，然后得到协方差矩阵的特征值特征向量，选择特征值最大(即方差最大)的k个特征所对应的特征向量组成的矩阵。这样就可以将数据矩阵转换到新的空间当中，实现数据特征的降维 得到协方差矩阵的特征值特征向量有两种方法：特征值分解协方差矩阵、奇异值分解协方差矩阵

特征值分解协方差矩阵

奇异值分解协方差矩阵

SVD奇异值分解

PCA数学原理

1
2
3
4
5
6
7
8
9
10
11
12
13
from sklearn.decomposition import PCA

pca=PCA(n_components=2)
X2D=pca.fit_transform(X)

"""
可以使用components_访问每一个主成分
每个主成分的方差解释率，可通过explained_variance_ratio_变量获得。它表示位于每个主成分轴上的数据集方差的比例。
"""
# 84.2% 的数据集方差位于第一轴，14.6% 的方差位于第二轴。第三轴的这一比例不到1.2％，
>>> print(pca.explained_variance_ratio_)
array([0.84248607, 0.14631839])

选择正确的维度

1
2
3
4
5
6
7
8
pca=PCA()
pac.fit(X)
cumsum=np.cumsum(pca.explained_variance_ratio_)
d=np.argmax(cumsum>=0.95)+1

# n_components设置为 0.0 到 1.0 之间的浮点数，表明您希望保留的方差比率
pca=PCA(n_components=0.95)
X_reduced=pca.fit_transform(X)

解压

1
2
3
pca=PCA(n_components=154)
X_mnist_reduced=pca.fit_transform(X_mnist)
X_mnist_recovered=pca.inverse_transform(X_mnist_reduced)

批量PCA

1
2
3
4
5
6
7
from sklearn.decomposition import IncrementalPCA

n_batches=100
inc_pca=IncrementalPCA(n_components=154)
for X_batch in np.array_split(X_mnist,n_batches):
    inc_pca.partial_fit(X_batch)
X_mnist_reduced=inc_pca.transform(X_mnist)

Randomized PCA

快速找到前d个主成分的近似值。它的计算复杂度是O(m × d^2) + O(d^3)，而不是O(m × n^2) + O(n^3)，所以当d远小于n时，它比之前的算法快得多

1
2
rnd_pca=PCA(n_components=154,svd_solver='randomized')
X_reduced=rnd_pca.fit_transform(X_mnist)

核 PCA（Kernel PCA）

1
2
3
4
from sklearn.decomposition import KernelPCA

rbf_pca=KernelPCA(n_components=2,kernel='rbf',gamma=0.04)
X_reduced=rbf_pca.fit_transform(X)

LLE

局部线性嵌入（Locally Linear Embedding）

1
2
3
4
from sklearn.manifold import LocallyLinearEmbedding

lle=LocallyLinearEmbedding(n_components=2,n_neighbors=10)
X_reduced=lle.fit_transform(X)